Here we are providing Class 7 Math Important Objective Chapter – 07 Congruence of Triangles because its very important for Class 7 students as we all know that every board exam question has MCQs so that students should practice these questions so that students can get good marks in board. Class 7 Math Important Objective Chapter – 07 Congruence of Triangles is an extremely important and its also a year in which students learn the fundamentals of concepts that help them lay a solid foundation for their higher education. Here we are providing in Class 7 Math Important Objective Chapter – 07 Congruence of Triangles 40+ questions so that students practice more and more. If you want class wise Notes Then Click Here
Class 7 Math Important Objective Chapter – 07 Congruence of Triangles
1. By which congruence property, the two triangles given are congruent?
(a) S.S.S Property
(b) R.H.S Property
(c) A. S.A Property
(d) S.A.S Property
Ans-(a)
2. ‘Under a given correspondence, two triangles are congruent if the three sides of the one are equal to the three corresponding sides of the other.’ The above is known as
(a) SSS congruence of two triangles
(b) SAS congruence of two triangles
(c) ASA congruence of two triangles
(d) RHS congruence of two right-angled triangles
Ans-(a)
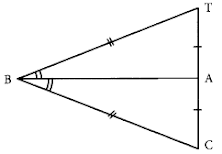
3. Complete the congruence statement ∆BCA ≅
(a) ∆BTA
(b) ∆BAT
(c) ∆ABT
(d) ∆ATB
Ans-(a)
4. What comes next in the sequence: 2, 4, 10, 28, ___ ?
(a) 64
(b) 70
(c) 76
(d) 82
Ans-(d)
5. ‘Under a given correspondence, two triangles are congruent if two sides and the angle included between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle.’
The above is known as
(a) SSS congruence of two triangles
(b) SAS congruence of two triangles
(c) ASA congruence of two triangles
(d) RHS congruence of two right-angled triangles
Ans-(b)
6. Two angles are congruent if they have
(a) Same name
(b) unequal measures
(c) equal measures
(d) none of these
Ans-(c)
7. ‘Under a given correspondence, two triangles are congruent if two angles and the side included between them in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle.’
The above is known as
(а) SSS congruence of two triangles
(b) SAS congruence of two triangles
(c) ASA congruence of two triangles
(d) RHS congruence of two right-angled triangles
Ans-(c)
8. Two figures are said to be congruent, if they have exactly the same:
(a) length and width
(b) shape and size
(c) area
(d) perimeter
Ans-(b)
9. What is the side included between the angles A and B in ΔABC?
(a) AC
(b) BC
(c) AB
(d) None of these
Ans-(c)
10. An angle is of 50° then its congruent angle is of:
(a) 40°
(b) 60°
(c) 50°
(d) None of these
Ans-(c)
11. ‘Under a given correspondence, two right-angled triangles are congruent if the hypotenuse and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg of the other triangle.’
The above is known as
(а) SSS congruence of two triangles
(b) SAS congruence of two triangles
(c) ASA congruence of two triangles
(d) RHS congruence of two right-angled triangles
Ans-(d)
12. ΔABC and ΔPQR are congruent under the correspondence: ABC ↔ RQP, then the part of ΔABC that correspond to ∠P is
(a) ∠A
(b) ∠C
(c) ∠B
(d) None of these
Ans-(b)
13. For two given triangles ABC and PQR, how many matchings are possible?
(a) 2
(b) 4
(c) 6
(d) 3
Ans-(c)
14. If the vertical angle of a isosceles triangle is 40°, then measure of other two angles will be
(a) 60°, 60°
(b) 80°, 80°
(c) 70°, 70°
(d) 45°, 45°
Ans-(c)
15. Are the following triangles congruent ?
(a) yes
(b) no
(c) none of these
Ans-(b)
16. The symbol for congruence is
(a) ≡
(b) ≅
(c) ↔
(d) =
Ans-(b)
17. Two triangles, A PQR and ADEF are of the same size and shape. What can we conclude about them?
(a) ΔPQR is smaller than ΔDFE.
(b) ΔPQR is larger than ΔDFE.
(c) ΔPQR is congruent to ΔDFE.
(d) ΔPQR is not congruent to ΔDFE.
Ans-(c)
18. The symbol for correspondence is
(a) =
(b) ↔
(c) ≡
(d) ≅
Ans-(b)
19. In ΔABC and ΔPQR, AB = 4 cm, BC = 5 cm, AC = 6 cm and PQ = 4 cm. QR = 5 cm. PR = 6 cm. then which of the following is true?
(a) ΔABC ≅ ΔQRP
(b) ΔABC ≅ ΔPQR
(c) ΔABC ≅ ΔRQP
(d) None of these
Ans-(b)
20. Given below are measurements of some parts of two triangles. Write the result in symbolic form if they are congruent.
In ΔABC,
∠A = 90°, AC = 5 cm, BC = 9 cm
In APQR,
∠P = 90°, PR = 3 cm QR = 8 cm
(a) are congruent
(b) are not congruent
Ans-(b)
21. If ∆ ABC = ∆ PQR, then ∠A corresponds to
(a) ∠P
(b) ∠Q
(c) ∠R
(d) none of these
Ans-(a)
22. In ΔABC and ΔDEF, AC = DF,AB = DE and BC=EF. By which property are ΔABC and ΔDEF congruent?
(a) R.H.S. property
(b) S.S.S. property
(c) S.A.S. property
(d) A.S.A. property
Ans-(b)
23. If the vertical angle of an isosceles triangle is 40°, then measure of other two angles will be
(a) 60°, 60°
(b) 80°, 80°
(c) 70°, 70°
(d) 45°, 45°
Ans-(c)
24. If ∆ ABC = ∆ PQR, then ∠B corresponds to
(a) ∠P
(b) ∠Q
(c) ∠R
(d) none of these
Ans-(b)
25. A triangle in which all three sides are of equal lengths is called _________.
(a) Isosceles
(b) Equilateral
(c) Scalene
(d) None of these
Ans-(b)
26. If ∆ ABC= ∆ PQR, then ∠C corresponds to
(a) ∠P
(b) ∠Q
(c) ∠R
(d) none of these
Ans-(c)
27. Which angle is included between the sides DE and EF of △DEF?
(a) ∠F
(b) ∠D
(c) ∠E
(d) None of these
Ans-(c)
28. We want to show that ∆ ART = ∆ PEN and we have to use SSS criterion. We have AR = PE and RT = EN. What more we need to show?
(a) AT = PN
(b) AT = PE
(c) AT = EN
(d) none of these
Ans-(a)
29. In the quadrilateral ABCD, AC = AD and AB bisect ∠A and ΔABC ≅ ΔABD. The relation between BC and BD is
(a) BC < BD
(b) BC > BD
(c) BC = BD
(d) None of these
Ans-(c)
30. We want to show that ∆ ART = ∆ PEN. We have to use SAS criterion. We have ∠T = ∠N, RT = EN. What more we need to show?
(a) PN = AT
(b) PN = AR
(c) PN = RT
(d) None of these
Ans-(a)
31. If ΔDEF ≅ ΔBCA, then the part of ΔBCA that correspond to ∠E is
(a) ∠B
(b) ∠C
(c) ∠A
(d) None of these
Ans-(b)
32. We want to show that ∆ ART = ∆ PEN. We have to use ASA criterion. We have AT = PN, ∠A = ∠P. What more we need to show?
(a) ∠T = ∠N
(b) ∠T = ∠E
(c) ∠T = ∠P
(d) None of these
Ans-(a)
33. Two students drew a line segment each. What is the condition for them to be congruent?
(a) They should be drawn with a scale.
(b) They should be drawn on the same sheet of paper.
(c) They should have different lengths.
(d) They should have the same length.
Ans-(d)
34. Which congruence criterion do you use in the following?
Given AC = DF
AB = DE
BC = EF
So, ∆ ABC ≅ ∆ DEF
(a) SSS
(b) SAS
(c) ASA
(d) RHS
Ans-(a)
35. The measure of each angle of an equilateral triangle is:
(a) 50°
(b) 70°
(c) 60°
(d) 100°
Ans-(c)
36. Which congruence criterion do you use in the following?
Given : ZX = RP
RQ = ZY
∠ PRQ = ∠ XZY
So, ∆ PRQ = ∆ XYZ
(a) SSS
(b) SAS
(c) ASA
(d) RHS
Ans-(b)
38. ΔABC is right triangle in which ∠A = 90° and AB = AC. The values of ∠B and ∠C will be
(a) ∠B = ∠C = 30°
(b) ∠B = ∠C = 50°
(c) ∠B = ∠C = 45°
(d) ∠B = ∠C = 60°
Ans-(c)
40. In the following figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆ RAT = ?
(a) ∆ WON
(b) ∆ WNO
(c) ∆ OWN
(d) ∆ ONW
Ans-(a)
40. Which of the following examines the congruence of plane figures?
(a) Trial and error method
(b) Superposition method
(c) Substitution method
(d) Transposition method
Ans-(b)
42. ΔABC and ΔPQR are congruent under the correspondence: ABC ↔ RPQ, then the part of ΔABC that correspond to PQ is
(a) AC
(b) AB
(c) BC
(d) None of These
Ans-(c)
43. For two given triangles ABC and PQR, how many matching are possible?
(a) 2
(b) 3
(c) 4
(d) 6
Ans-(d)
44. What is the angle included between the sides PN and PM of ΔMNP?
(a) ∠M
(b) ∠N
(c) ∠P
(d) None of these
Ans-(c)
45. In the given figure, if AB = AC and BD = DC then ∠ADC =
(a) 45°
(b) 60°
(c) 125°
(d) 90°
Ans-(d)
46. Complete the congruence statement ∆ BCA = ?
(a) ∆ BTA
(b) ∆ BAT
(c) ∆ ABT
(d) ∆ ATB
Ans-(a)